Home | Violal 1

Papers

My research focuses on Equivariant Degree Theory, a branch of nonlinear analysis at the intersection of partial differential equations, dynamical systems, and algebraic topology. Below are some of my papers.

Octahedral Molecule studies the nonlinear dynamics of molecules with octahedral symmetry. By applying method of equivariant gradient degree and slice principle (see Rybicki and Krawcewicz), it analyzes a Newtonian system exhibiting temporal and spatial symmetries under the group O(2)×S4×Z2×O(3). The study proves the existence of branches of periodic solutions bifurcating from the critical orbit of equilibrium, with at least 16 distinct symmetry types. It significantly extends the vibrational modes identified in theoretical studies Bush of Vibrational Modes for Octahedral System and SF6 with Density Function Theory (by GM Chechin et al.) Please start from here to see all nonlinear vibrational modes detected.

Global Bifurcation of Coupled Bose-Einstein Condensate (with Wiesław Krawcewicz, Carlos García Azpeitia, Anna Gołębiewska) studies a four component BEC system governed by Gross-Pitaevskii equations, which admits symmetry of O(3)×S4. In our setting, simple critical values yield kernel dimensions of 3(2k+1) for k∈N+, introducing substantial analytical challenges. We resolve this by leveraging tools equivariant gradient degree and Euler ring homomorphisms. This framework resovles the complexity and also reveals, in the case k=1, the presence of at least 6 bifurcating branches with distinct symmetry types.

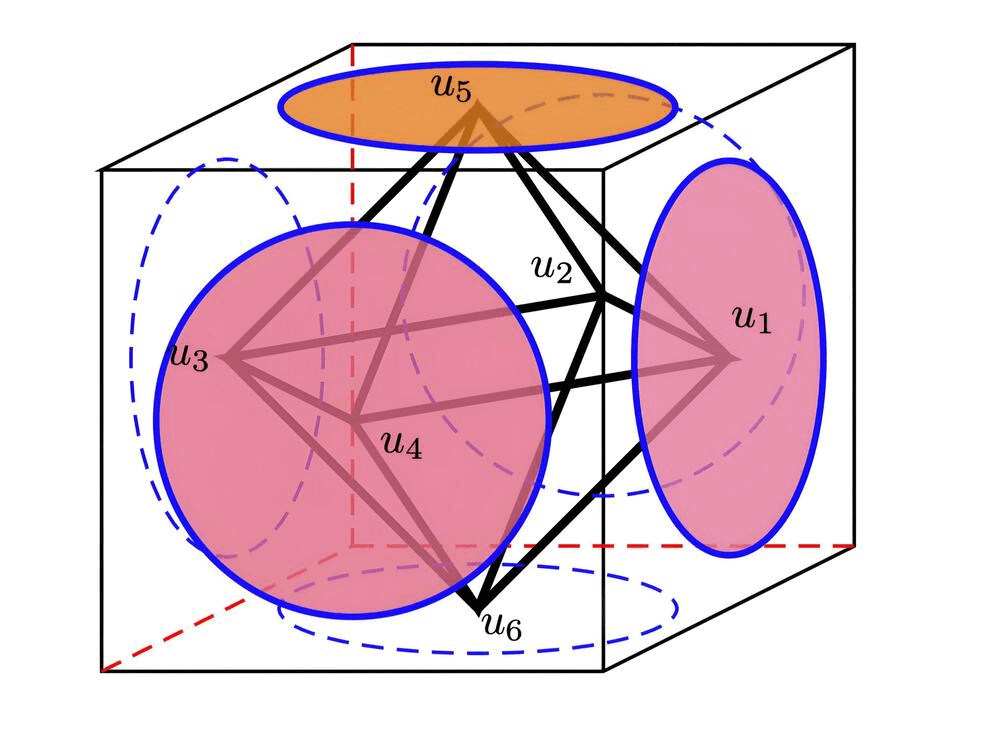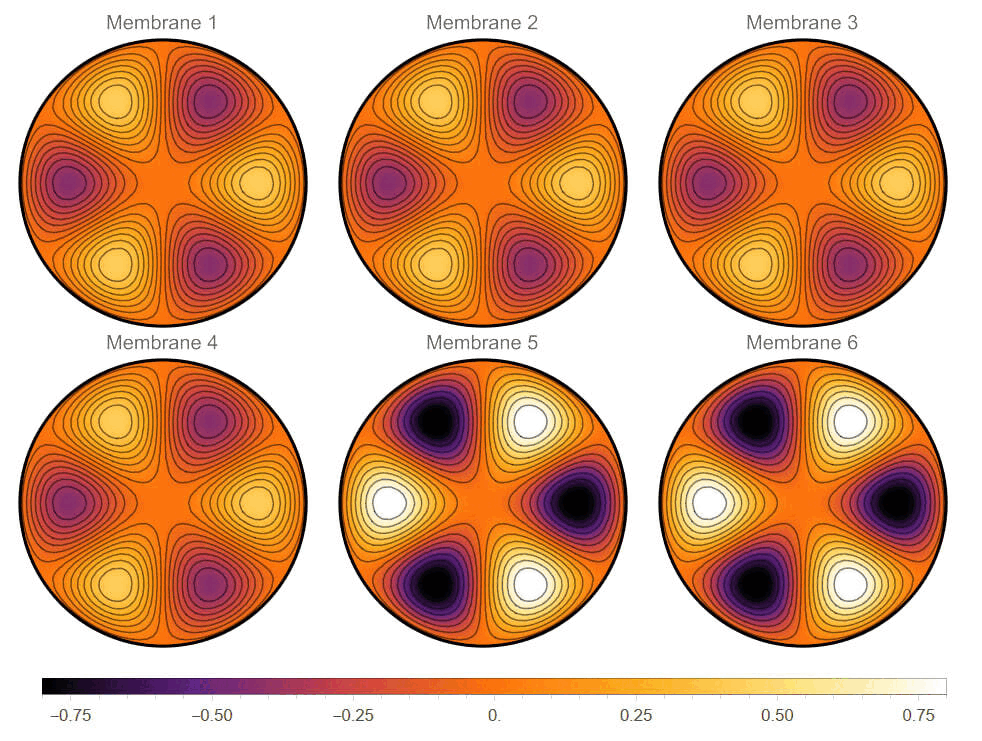
Global Bifurcation of Non-Radial Solutions On Unit Disc in R^2 (with Ziad Ghanem, Casey Crane) establishes a global bifurcation result for elliptic problem −Δu=f(α,z,u) with Dirichlet boundary conditions on the unit disc D:={z∈C:∣z∣<1}. The nonlinearity f is assumed to be O(2) invariant and Γx Z2 equivariant. Using Leray–Schauder degree theory, we demonstrate the existence of non-radial solutions bifurcating from the trivial one. To illustrate the abstract results, we consider a concrete example inspired by the vibration of membranes with cubical coupling.

Existence of Non-Radial Solutions On Unit Ball in R^3 (with Wiesław Krawcewicz, Carlos García Azpeitia) proves the existence of non-radial solutions to the problem −△u = f (x, u), u|∂Ω = 0 on Ω := {x ∈ R3: ‖x‖ < 1}, where f admits O(3)xZ2 symmetry. Although Golubitsky theoretically addresses representation and symmetry breaking from O(3), the significantly greater complexity of O(3) compared to O(2) has posed substantial challenges. This work presents, for the first time, explicit computations of the maximal isotropy types associated with each isotypic component under the action of O(3) and its extension O(3)×Z2.